© Viviane Desgrange.
Snapshots of the Grab superapp to which I contributed as a software engineer.
My work involved the back-end development of the communication services used by the customers, drivers and company employees to communicate through the app.
Snapshots of the user interface to which I contributed as a front-end software engineer.
Most of the real-world physical phenomena can be described by mathematical models governed by partial differential equations (PDE). These differential equations might be too complex to be solved analytically, therefore requiring advanced computational capabilities to be solved numerically. This defines the field of Scientific Computing. The main drawbacks lies in the fact that these Full-Order Models (FOM) require large range of parameters, solved on high-dimensional grid and using small time steps to performed accurate simulations able to capture the sharpest details, such that the computational resources involved are a bottleneck on large-scale application. Multiples methods of Model Order Reduction (MOR) were implemented to avoid these difficulties. Instead of solving the FOM, these are Reduced order models (ROM), able to capture the main dynamics while reducing the complexity of the system, which are numerically solved. These ROM usually trade accuracy for time complexity and require a closure term to capture the information loss which occurred when reducing the system. In the past decade, the progress in the field of machine learning brings to light new techniques either to learn these closure terms or to learn new type of ROM, such as the right-hand side of a PDE.
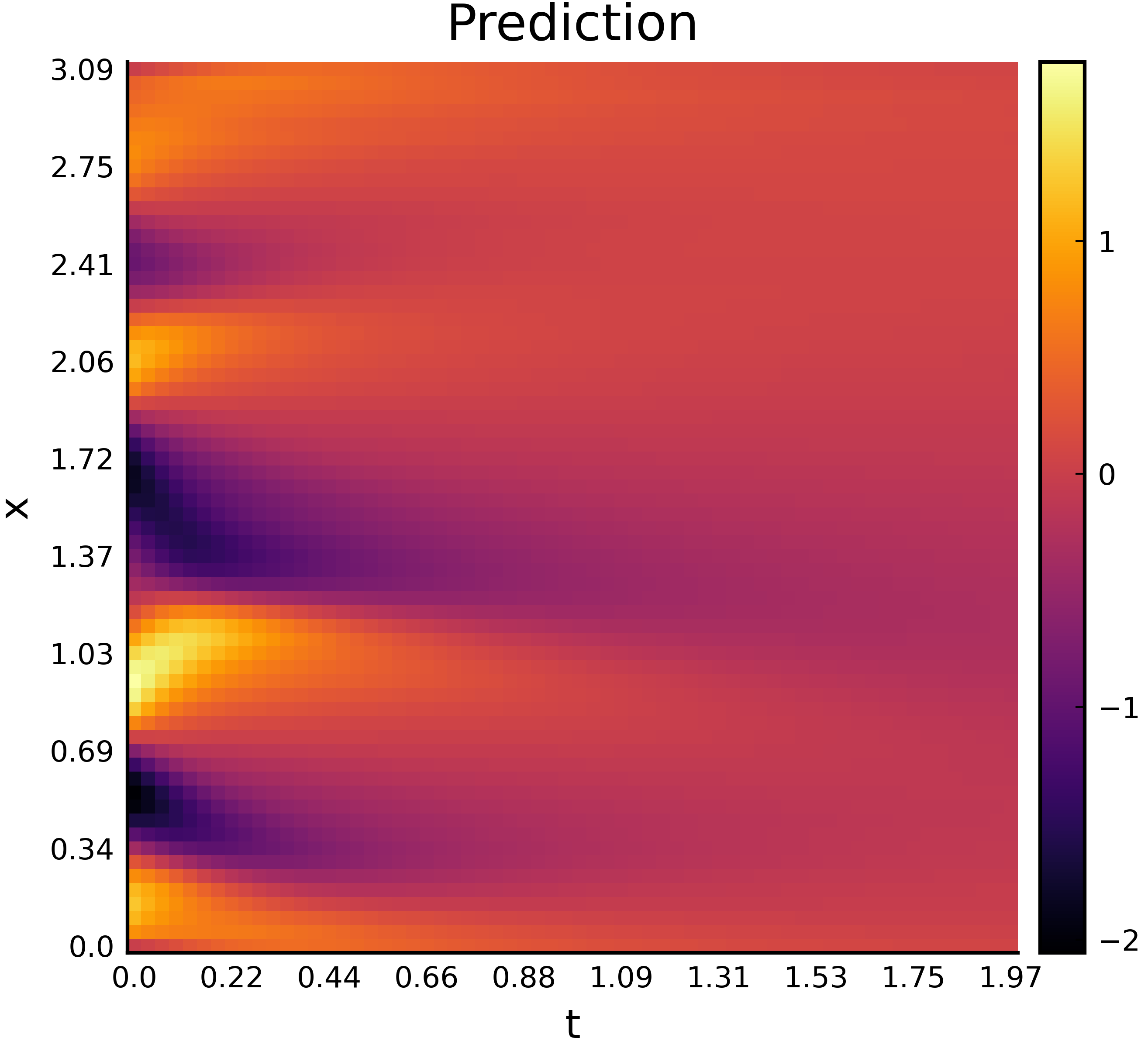
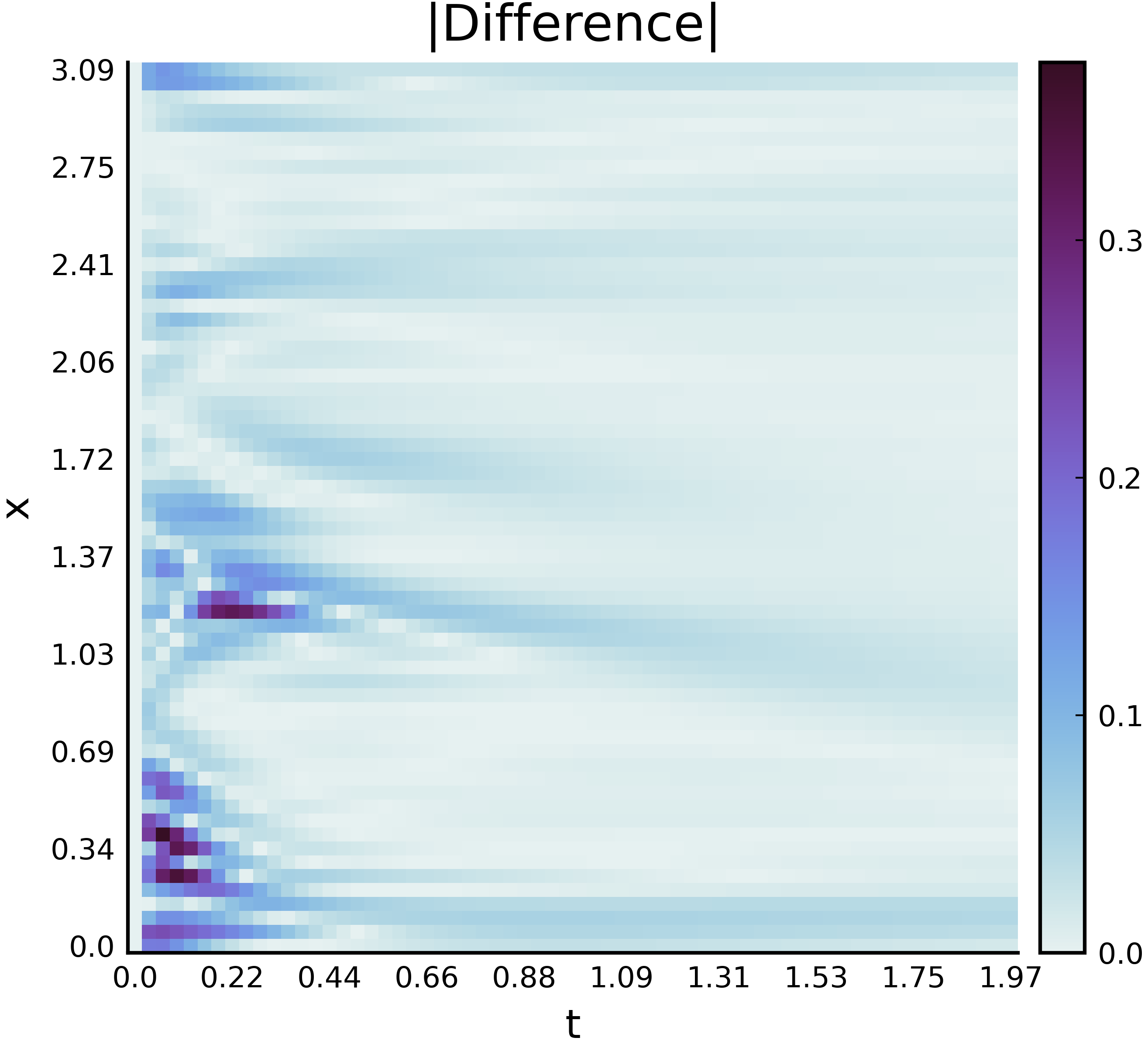
This thesis, beside reviewing the existing MOR methods, aims at assessing some of the machine learning techniques which rise in the recent years applied to simple linear and non-linear PDEs on coarse grid. It investigates how models should be adapted to the problem considered, how to parameterize them to accurately approximate the FOM, with an emphasis on the inverse problem aspect of the methods employed during training.
See here for complete document
A personal project done to refresh modern C++ skills, gather knowledge about the Vulkan cross-platform API and work with GPU. A long term goal would be to render fluid flows solutions combined with PINN. Source are available here.

